Ineffable cardinal

In the mathematics of transfinite numbers, an ineffable cardinal is a certain kind of large cardinal number, introduced by Jensen & Kunen (1969).

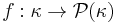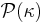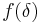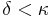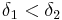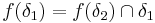A cardinal number \kappa is called almost ineffable if for every f: \kappa \to \mathcal{P}(\kappa) (where \mathcal{P}(\kappa) is the powerset of \kappa) with the property that f(\delta) is a subset of \delta for all ordinals \delta < \kappa, there is a subset S of \kappa having cardinal \kappa and homogeneous for f, in the sense that for any \delta_1 < \delta_2 in S, f(\delta_1) = f(\delta_2) \cap \delta_1.

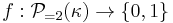A cardinal number \kappa is called ineffable if for every binary-valued function f�: \mathcal{P}_{=2}(\kappa) \to \{0,1\}, there is a stationary subset of \kappa on which f is homogeneous: that is, either f maps all unordered pairs of elements drawn from that subset to zero, or it maps all such unordered pairs to one.

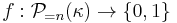More generally, \kappa is called n-ineffable (for a positive integer n) if for every f�: \mathcal{P}_{=n}(\kappa) \to \{0,1\} there is a stationary subset of \kappa on which f is n-homogeneous (takes the same value for all unordered n-tuples drawn from the subset). Thus, it is ineffable if and only if it is 2-ineffable.

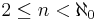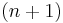A totally ineffable cardinal is a cardinal that is n-ineffable for every 2 \leq n < \aleph_0. If \kappa is (n%2B1)-ineffable, then the set of n-ineffable cardinals below \kappa is a stationary subset of \kappa.

Totally ineffable cardinals are of greater consistency strength than subtle cardinals and of lesser consistency strength than remarkable cardinals. A list of large cardinal axioms by consistency strength is available here.

References